This is an LLM-translated blog post from the original slides titled "时髦智能体能搞定玄学符号回归吗?". The image above is sourced from the DeepMind blog.
Imagine discovering Kepler's laws from planetary motion data alone, without prior knowledge of gravity. This is the essence of symbolic regression: constructing interpretable and concise mathematical expressions from limited data. This task faces significant challenges due to the vast and discrete search space of possible expressions, where overfitting and local optima are common pitfalls. Recent advances in AI agents have sparked interest in whether these systems can overcome these longstanding difficulties. This post examines the intersection of modern AI agents with symbolic regression, evaluating both their potential and limitations through a critical lens.
AlphaEvolve: Hype and Limitations #
Released by Google DeepMind in May 2025, AlphaEvolve leverages the Gemini 2.0 large language model to improve various algorithms, including matrix multiplication, geometric optimization, and acceleration of FlashAttention implementations. For example, the system demonstrated improvements in matrix multiplication operations, reducing the count from 87 to 85 for a 4×4×7 matrix, from 98 to 96 for a 4×4×8 matrix, and from 93 to 90 for a 4×5×6 matrix.
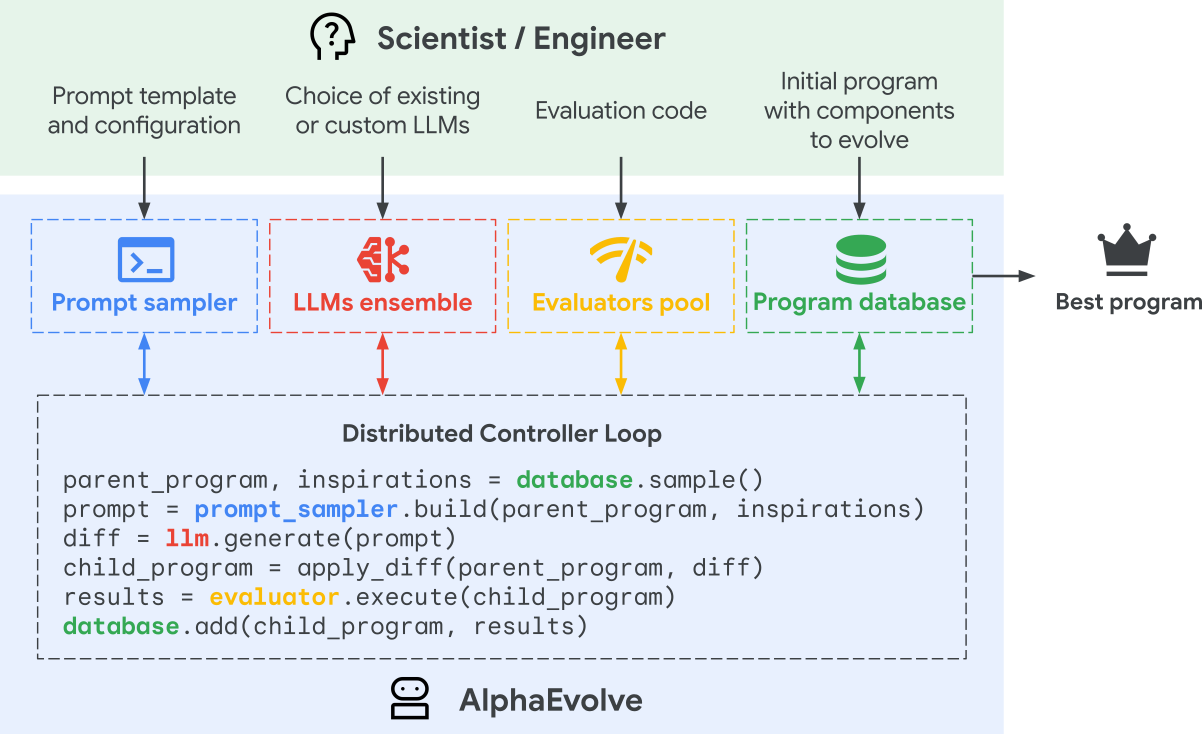
AlphaEvolve employs an iterative evolutionary process where the LLM modifies code based on performance feedback. Its prompt engineering consists of essential components (system instructions and previously sampled programs) and optional components (performance metrics, problem context, meta-prompts for prompt updating, and randomly set prompts).
Despite its promising architecture, AlphaEvolve faces significant transparency issues. DeepMind has not disclosed critical technical details, withheld the framework code from public release, and shifted focus toward commercialization through early access programs and UI development.
Independent replication attempts, such as those using OpenEvolve for circle packing problems, only reproduce the previous state-of-the-art value of 2.634 instead of AlphaEvolve's reported improvement to 2.635. This discrepancy suggests caution is warranted before embracing AI agents as complete solutions to symbolic regression challenges.
Established Symbolic Regression Approaches #
The search space of symbolic regression is discrete and grows combinatorially with expression length and operator complexity. Since we only have a limited data, it's easy to overfit them. And the optimization can fell in local optima that prevents us finding the simple and interpretable expression.
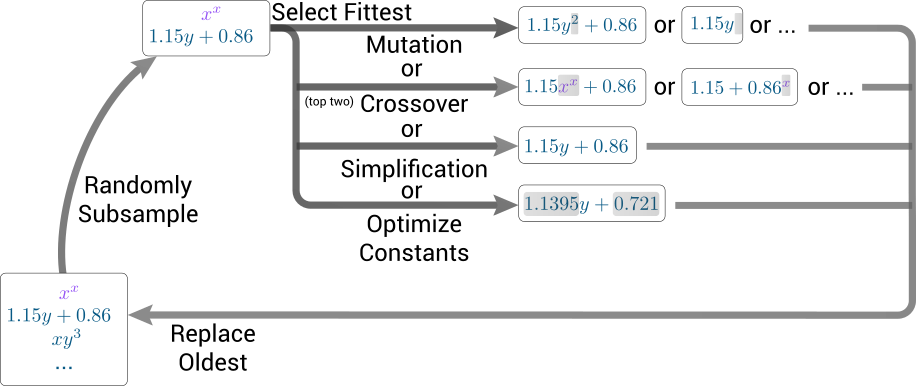
Genetic Algorithms (PySR) #
PySR implements evolutionary operations—mutation, crossover, selection, and elimination—to evolve expression trees [M. Cranmer, arXiv.2305.01582]. The approach incorporates several mechanisms to avoid premature convergence: simulated annealing (allowing acceptance of poorer individuals early in the process), age regularization (preventing entrapment in local optima), post-evolution simplification and constant optimization, automatic adjustment of complexity penalties, and island algorithms for robustness and parallelization.
When evaluated against the EmpiricalBench suite of physics formulas, PySR correctly recovered 5/5 solutions for Hubble's law, Kepler's third law, Newton's gravity, Leavitt's law, Schechter's function, Bode's law, and the ideal gas law. However, it failed to recover Planck's radiation law and the Rydberg formula in all test cases.
| Name | Formula | PySR |
|---|---|---|
| Hubble | 5/5 | |
| Kepler | 5/5 | |
| Newton | 5/5 | |
| Planck | 0/5 | |
| Leavitt | 5/5 | |
| Schechter | 5/5 | |
| Bode | 5/5 | |
| Ideal Gas | 5/5 | |
| Rydberg | 0/5 |
PySR's key characteristics include:
- Representation: Expression trees
- Complexity control: Penalty terms in fitness function
- Dimensional analysis: Not implemented
- Constant optimization: Dedicated optimization algorithms
- High-dimensional handling: Gradient boosting trees
While PySR benefits from efficient parallel computation and requires no prior assumptions about expressions, it suffers from weak local optimization capabilities, limited interpretability of the evolutionary process, and difficulties handling high-dimensional problems. The computational demands remain substantial, requiring sufficiently large populations and iterations that can necessitate running each island on a separate node.
Brute-Force Search (SISSO) #
The SISSO algorithm assumes target expressions are linear combinations of generated features [R. Ouyang et al., PRM 2, 083802 (2018)]. It repeatedly applies operators to create a vast feature space that can reach or more elements even when dimensional analysis is applied. The method employs a two-step approach: Sure Independence Screening (SIS) selects features most correlated with the target property, followed by Sparsifying Operator (SO) techniques like LASSO (-norm approximation) or -norm minimization to combine features linearly.

SISSO has demonstrated success in predicting binary compound enthalpies with 82 materials and 32 features, outperforming commercial tools like Eureqa.
SISSO's key characteristics include:
- Representation: Linear combinations of features
- Complexity control: Feature space size and expression order
- Dimensional analysis: Implemented
- Constant optimization: LASSO/ methods
- High-dimensional handling: Iterative variable selection
While SISSO systematically explores large feature spaces, its assumption of linear combinations limits expressiveness. Computational demands escalate rapidly with variable count, and iterative variable selection is necessary to manage computational overhead.
Reinforcement Learning (-SO) #
-SO employs RNNs with reinforcement learning to maximize rewards for valid expressions, with an "in-situ" mechanism that restricts token output to ensure dimensional correctness. The approach uses a risk-seeking policy gradient objective to maximize the expectation of rewards in the best cases. When evaluated against the Feynman benchmark, -SO demonstrated competitive performance.
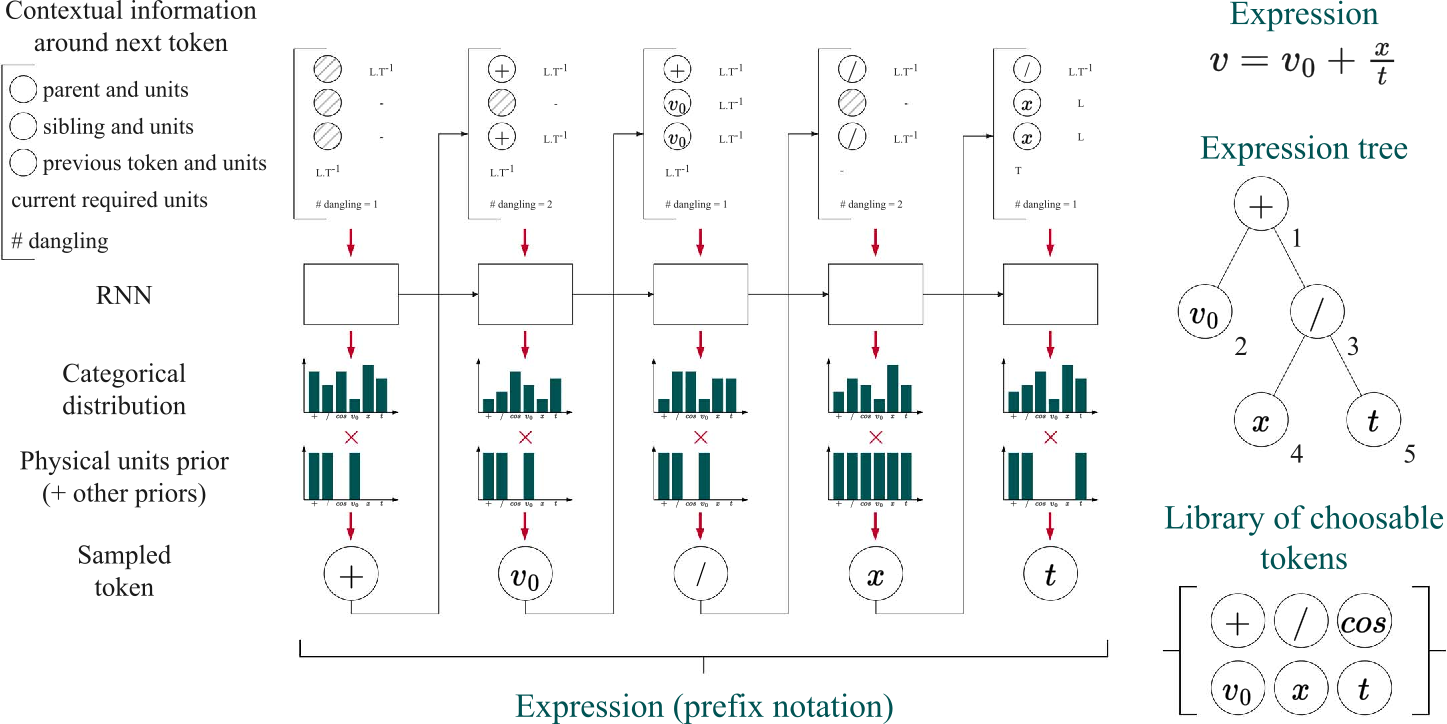
-SO's key characteristics include:
- Representation: Expression trees (as token sequences)
- Complexity control: Token count limitation
- Dimensional analysis: Implemented
- Constant optimization: Dedicated optimization algorithms
- High-dimensional handling: Not addressed
While -SO requires no prior assumptions about expressions and demonstrates robustness to noisy data, it depends on prior assumptions about constant dimensions and suffers from token sequences being an imperfect representation of mathematical equivalence (e.g., vs. ). Like other methods, it cannot guarantee finding global optima and requires retraining for each new problem.
Integrating AI Agents with Symbolic Regression #
Concept-Guided Search (LaSR) #
LaSR employs large language models to extract concepts from high-performing expressions and guide PySR's evolutionary process. The approach involves three steps: the LLM extracts concepts from successful expressions, generates new concepts based on these, and then evolves expressions using either classic genetic algorithms or LLM-guided evolution.
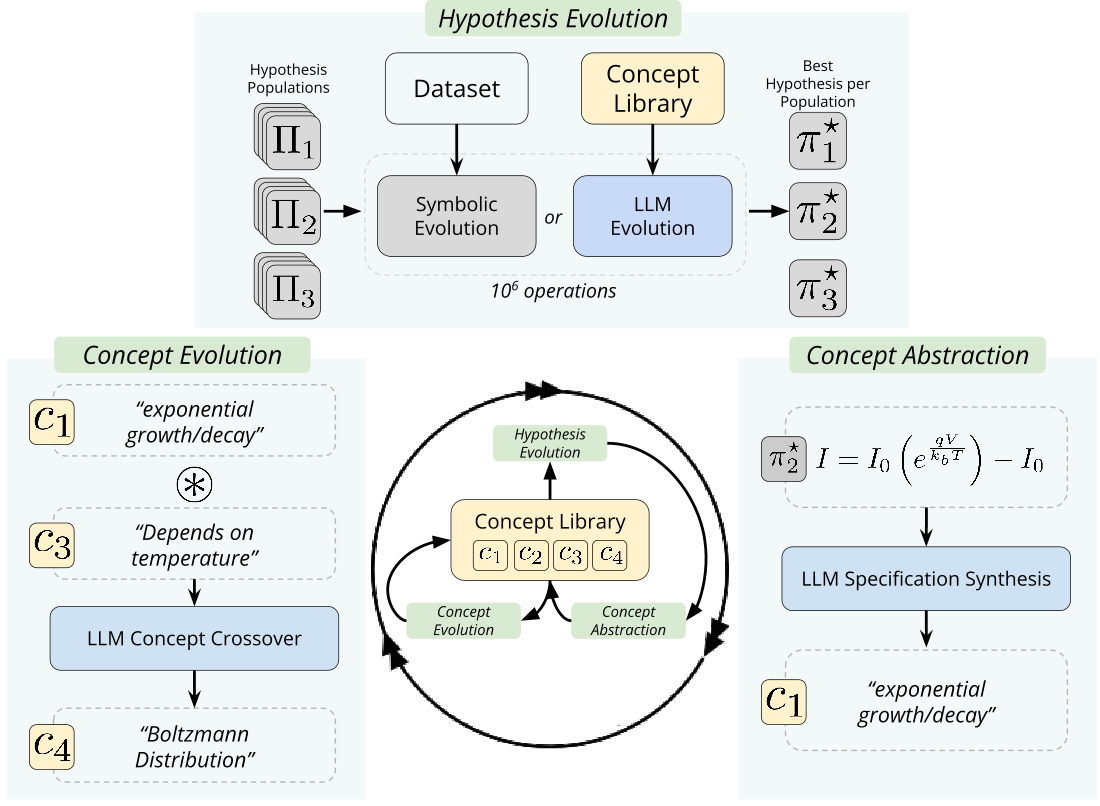
When evaluated on the Feynman dataset over 40 iterations, LaSR increased exact matches from 59 (PySR) to 72 (GPT-3.5), with corresponding reductions in almost matches (from 7 to 3) and close matches (from 16 to 10).
| Type | PySR | LaSR (Llama3-8B) | LaSR (GPT-3.5) |
|---|---|---|---|
| Exact | 59 | 67 | 72 |
| Almost | 7 | 5 | 3 |
| Close | 16 | 9 | 10 |
| Fail | 18 | 19 | 15 |
LaSR's key characteristics include:
- Representation: Expression trees or strings
- Complexity control: Penalty terms in fitness function
- Dimensional analysis: Not implemented
- Constant optimization: Same as PySR
- High-dimensional handling: Same as PySR
The primary advantages of LaSR are its ability to learn concepts that better guide genetic algorithms and improved interpretability of the evolutionary process compared to traditional approaches. However, it cannot guarantee the LLM learns correct concepts, depends heavily on LLM capabilities, and struggles to fully leverage LLM potential since the expression string is not a field LLMs are good at. Computationally, LLM-guided evolution constitutes only a small portion of the overall process since the LLMs are computationally expensive.
LLM-Driven Search (LLM-SR) #
LLM-SR represents a paradigm shift by using large language models as active search agents. The method operates iteratively: the LLM proposes candidate expressions based on problem descriptions, input variables, and performance feedback, then evaluates them against the data. Through island-based parallelization, LLM-SR maintains a diverse pool of high-performing solutions.
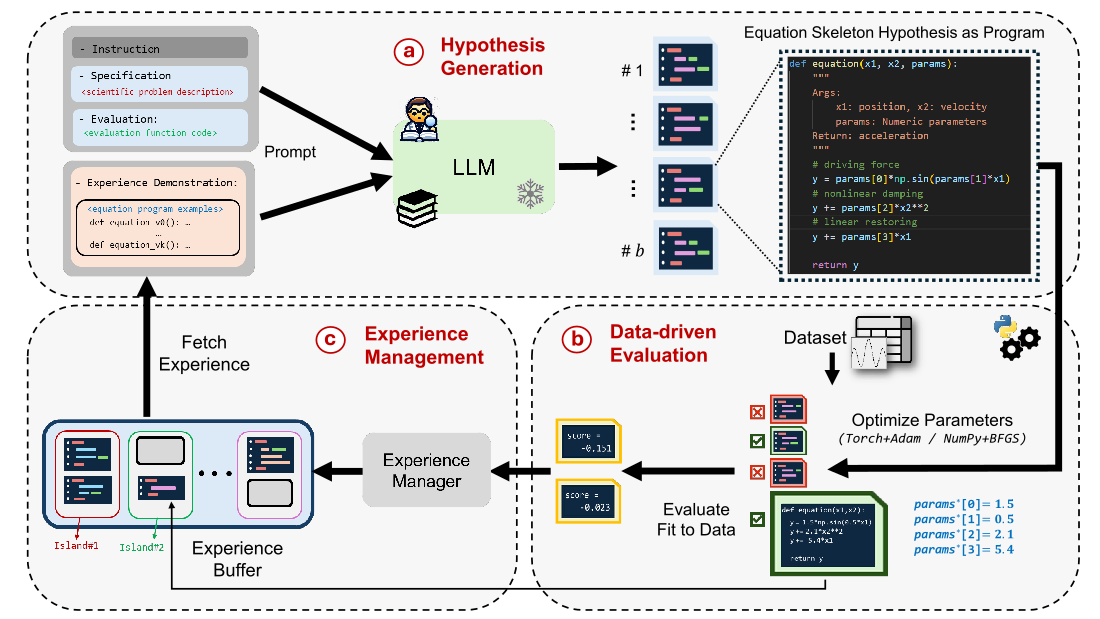
LLM-SR has demonstrated strong performance on synthetic benchmarks, such as recovering stress-strain relationships in aluminum across temperatures, often reaching high-accuracy solutions in fewer iterations compared to traditional methods. On the oscillation benchmark, LLM-SR achieved a mean-squared error of 4.65e-7 on in-distribution data and 0.0005 on out-of-distribution data, significantly outperforming other methods.
| Model | ID | OOD |
|---|---|---|
| DSR | 0.0087 | 0.2454 |
| uDSR | 0.0003 | 0.0007 |
| PySR | 0.0009 | 0.3106 |
| FunSearch | 0.4840 | 8.059 |
| LLM-SR | 4.65e-7 | 0.0005 |
| no optim. | 0.1371 | 0.6764 |
| no prior | 0.0001 | 0.0029 |
| no program | 0.0001 | 0.0035 |
LLM-SR's key characteristics include:
- Representation: Code
- Complexity control: Number of input parameters
- Dimensional analysis: LLM-dependent
- Constant optimization: Dedicated optimization algorithms
- High-dimensional handling: Not addressed
While LLM-SR effectively leverages the LLM's prior knowledge and can propose contextually appropriate expressions, it depends heavily on the LLM's capabilities, cannot directly simplify expressions or measure diversity, and relies on synthetic datasets for benchmarking, raising concerns about real-world applicability.
FunSearch: The AlphaEvolve Precursor #
FunSearch, developed by DeepMind as AlphaEvolve's predecessor, performs poorly on symbolic regression tasks. In oscillation benchmarks, it achieved a mean-squared error of 0.4840 on in-distribution data versus LLM-SR's 4.65e-7. This demonstrates that general-purpose LLM search frameworks require domain-specific adaptations to succeed in symbolic regression.
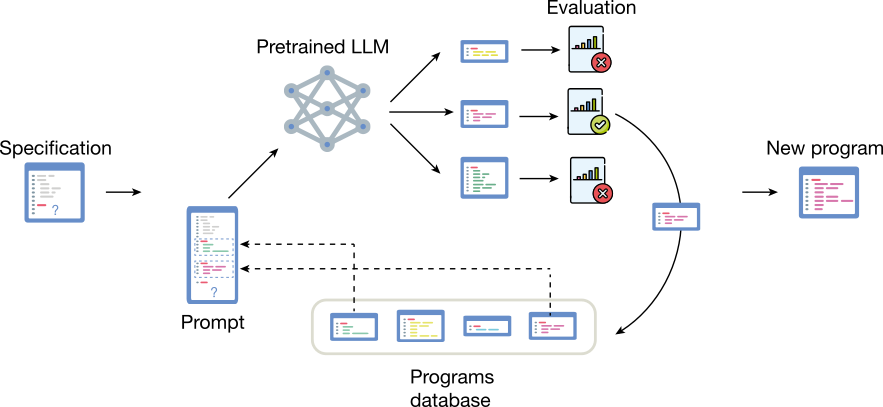
FunSearch's key characteristics include:
- Representation: Code
- Complexity control: Kolmogorov complexity
- Dimensional analysis: LLM-dependent
- Constant optimization: LLM-dependent
- High-dimensional handling: Not addressed
Comparative Analysis #
Conclusions #
While AI agents enhance symbolic regression capabilities, they function best as complementary tools rather than complete solutions. Progress in this field requires combining domain expertise with methodological innovation, maintaining realistic expectations about the persistent challenges of expression discovery.